TEMA 11: Clase Math.
1.- Metodo de la clase Math.
Para utilizar esta clase, debemos escribir Math.método(parámetros); donde método sera uno de los siguientes y parámetros aquellos que tengamos que usar. Un método puede estar sobrescrito para distintos tipos de datos.
Recuerda que si almacenas el resultado de la función, debe coincidir con el tipo de la variable.
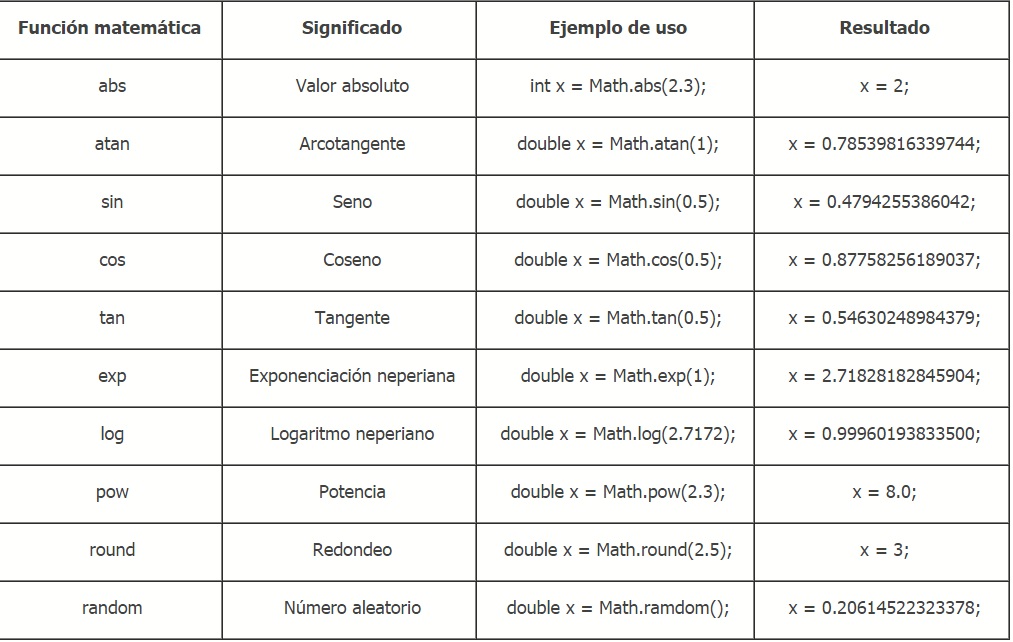
Veamos algún ejemplo:
public class PruebaApp {
public static void main(String[] args) {
double operador1=25.5;
double operador2=15.21;
System.out.println(Math.ceil(operador1)); // Devuelve 26.0
System.out.println(Math.floor(operador2)); //Devuelve 15.0
System.out.println(Math.pow(operador1, operador2)); // Devuelve 2.474435537975361E21
System.out.println(Math.max(operador1, operador2)); //Devuelve 25.5
System.out.println(Math.sqrt(operador1)); ////Devuelve 5.049752469181039
}
}
Miembros dato constantes
La clase Math define dos constantes muy útiles, el número p y el número e.public final class Math {
public static final double E = 2.7182818284590452354;
public static final double PI = 3.14159265358979323846;
//...
}
El modificador final indica que los valores que guardan no se pueden cambiar, son valores constantesSe accede a estas constantes desde la clase Math, de la siguiente forma
System.out.println("Pi es " + Math.PI);
System.out.println("e es " + Math.E);
Funciones miembro
La clase Math define muchas funciones y versiones distintas de cada función.Por ejemplo, para hallar el valor absoluto de un número define las siguientes funciones. Se llama a una u otra dependiendo del tipo de dato que se le pasa en su único argumento.
public final class Math {
public static int abs(int a) {
return (a < 0) ? -a : a;
}
public static long abs(long a) {
return (a < 0) ? -a : a;
}
public static float abs(float a) {
return (a < 0) ? -a : a;
}
public static double abs(double a) {
return (a < 0) ? -a : a;
}
//...
}
Por ejemplo, hallar el valor absoluto de los siguientes números int i = -9;
double x = 0.3498;
System.out.println("|" + i + "| es " + Math.abs(i));
System.out.println("|" + x + "| es " + Math.abs(x));
Math.abs(i), llama a la primera versión, y Math.abs(x) llama a la última versión.Funciones trigonométricas
En las funciones trigonométricas los argumentos se expresan en radianes. Por ejemplo, el ángulo 45º se convierte en radianes y luego se halla el seno, el coseno y la tangente double angulo = 45.0 * Math.PI/180.0;
System.out.println("cos(" + angulo + ") es " + Math.cos(angulo));
System.out.println("sin(" + angulo + ") es " + Math.sin(angulo));
System.out.println("tan(" + angulo + ") es " + Math.tan(angulo));
Para pasar de coordenadas rectangulares a polares es útil la función atan2, que admite dos argumentos, la ordenada y la abscisa del punto. Devuelve el ángulo en radianes. double y=-6.2; //ordenada
double x=1.2; //abscisa
System.out.println("atan2(" + y+" , "+x + ") es " + Math.atan2(y, x));
Funciones exponencial y logarítmica
La función exponencial exp devuelve el número e elevado a una potencia System.out.println("exp(1.0) es " + Math.exp(1.0));
System.out.println("exp(10.0) es " + Math.exp(10.0));
System.out.println("exp(0.0) es " + Math.exp(0.0));
La función log calcula el logaritmo natural (de base e) de un número System.out.println("log(1.0) es " + Math.log(1.0));
System.out.println("log(10.0) es " + Math.log(10.0));
System.out.println("log(Math.E) es " + Math.log(Math.E));
Función potencia y raíz cuadrada
Para elevar un número x a la potencia y, se emplea pow(x, y) System.out.println("pow(10.0, 3.5) es " + Math.pow(10.0,3.5));
Para hallar la raíz cuadrada de un número, se emplea la función sqrt System.out.println("La raíz cuadrada de " + x + " is " + Math.sqrt(x));
Aproximación de un número decimal
Para expresar un número real con un número especificado de números decimales empleamos la función round. Por ejemplo, para expresar los números x e y con dos cifras decimales escribimos double x = 72.3543;
double y = 0.3498;
System.out.println(x + " es aprox. " + (double)Math.round(x*100)/100);
System.out.println(y + " es aprox. " + (double)Math.round(y*100)/100);
Se obtiene 72.35 y 0.35 como cabría esperar. Fijarse que round devuelve un número entero int que es necesario promocionar a double para efectuar la división entre 100.Si empleamos la función floor en vez de round obtendríamos
System.out.println(x + " es aprox. " + Math.floor(x*100)/100);
System.out.println(y + " es aprox. " + Math.floor(y*100)/100);
Se obtiene 72.35 y 0.34. La aproximación del primero es correcta ya que la tercera cifra decimal es 4 inferior a 5. La aproximación del segundo es incorrecta ya que la tercera cifra decimal es 9 mayor que 5. En la mayor parte de los cálculos se cometen errores, por lo que la diferencia entre floor y round no es significativa.El mayor y el menor de dos números
Para hallar el mayor y el menor de dos números se emplean las funciones min y max que comparan números del mismo tipo. int i = 7;
int j = -9;
double x = 72.3543;
double y = 0.3498;
// para hallar el menor de dos número
System.out.println("min(" + i + "," + j + ") es " + Math.min(i,j));
System.out.println("min(" + x + "," + y + ") es " + Math.min(x,y));
// Para hallar el mayor de dos números
System.out.println("max(" + i + "," + j + ") es " + Math.max(i,j));
System.out.println("max(" + x + "," + y + ") es " + Math.max(x,y));
Números aleatorios
La clase Math define una función denominada random que devuelve un número pseudoaleatorio comprendido en el intervalo [0.0, 1.0). Existe otra alternativa, se pueden generar números pseudoaleatorios a partir de un objeto de la clase Random, que llame a la función miembro nextDouble. System.out.println("Número aleatorio: " + Math.random());
System.out.println("Otro número aleatorio: " + Math.random());
Cálculo del número irracional p
pi:Para hallar la longitud de una circunferencia de radio R, primero se calcula el perímetro de un triángulo equilátero (3 lados) inscrito en dicha circunferencia, luego, de un hexágono (6 lados), un dodecágono (12 lados), y así sucesivamente. El límite de la sucesión de perímetros es precisamente la longitud de la circunferencia 2p R.
Si tomamos una circunferencia de radio unidad, al dividir entre dos los valores de los perímetros iremos obteniendo las sucesivas aproximaciones del número irracional p .
| A partir de la figura, podemos calcular la longitud del lado an un polígono regular de n lados inscrito en la circunferencia de radio R, (en color rojo). Del mismo modo, obtenemos la longitud del lado de un polígono regular inscrito de 2n lados (en color azul). |
Establecemos la relación entre an y a2n y por tanto, entre el perímetro Pn del polígono regular de n lados y el perímetro P2n del polígono regular de 2n lados.
Tomando como radio R, la unidad
- Para un triángulo, n=3, la longitud del lado es a3=2sen60º, y el perímetro
- Para un hexágono, n=6, la longitud del lado es a6=2sen30º=1, y el perímetro P6=6.
- y así sucesivamente.
- Partimos del valor del perímetro P de un triángulo equilátero inscrito en una circunferencia de radio unidad, el valor de n es 3.
- Calculamos el perímetro P de un polígono de 2n lados a partir del valor del perímetro de un polígono regular de n lados.
- El valor obtenido P será el valor del perímetro de un polígono regular de n=2n lados.
- Se imprime el valor de P dividido entre dos (aproximación de p)
- Se vuelve al paso 2.
En primer lugar, hemos de tener en cuenta que la expresión
Por ejemplo si n es tipo de dato int. Al evaluar el denominador en la primera expresión obtenemos el cuadrado de n que crece muy rápidamente con n, sobrepasándose (overflow) el valor máximo que puede guardar una variable entera dado por Integer.MAX_VALUE. Integer es la clase que describe los números enteros. Por tanto, al realizar los cálculos en el ordenador es aconsejable emplear la segunda expresión en vez de la primera, incluso si cambiamos el tipo de dato de n de int a long.
El cálculo de p implica un número infinito de iteracciones, ya que como hemos visto no es posible al sobrepasarse el valor máximo que puede guardar una variable entera, nuestra primera intención sería la programar un bucle que realice el máximo número de iteracciones
double perimetro=3*Math.sqrt(3); //triángulo equilátero inscrito
long n=3;
int i=0; //número de iteracciones
while(n<Long.MAX_VALUE){
perimetro=2*n*Math.sqrt(2.0-Math.sqrt(4.0-(perimetro/n)*(perimetro/n)));
n=2*n;
i++;
System.out.println(i+" -- "+perimetro/2);
}
Con cierta sorpresa observamos la salida del programa cuando se ha completado el bucle, se imprime un cero, en vez de 3.14159265358979323846.Si observamos las 30 primeras iteracciones vemos, tal como se muestra en la figura inferior, que la valor más próximo a p se obtiene en las iteracciones 13, 14, 15, y 16.
while(i<30){
//...
}

Comentarios
Publicar un comentario